Puedes estudiar la historia de dos formas, bien cronológicamente, bien a través de sus distintas ramas.

Cronológicamente, esta historia podría dividirse en cuatro grandes bloques según la periodicidad establecida por A.N. Kolmogorov:

a) Nacimiento de las matemáticas: Este periodo se prolonga hasta los siglos VI-V a.C. cuando las matemáticas se conviertesn en una ciencia independiente con objeto y metodología propios. También podría denominarse matemáticas antiguas o prehelénicas y en ella se suelen englobar las matemáticas de las antiguas civilizaciones de Egipto, Mesopotamia, China e India. Grecia estaría situada a caballo entre este periodo y el siguiente.

Antes de la edad moderna y la dispersión del conocimiento a lo largo del mundo, los ejemplos escritos de nuevos desarrollos matemáticos salían a la luz sólo en unos pocos escenarios. La textos matemáticos más antiguos disponibles son el plimpton 322 (Matemáticas en Babilonia c. 1900 a.C.), el Papiro de Moscú (Matemáticas en el Antiguo Egipto c. 1850 a.C.), el Papiro de Rhind (Matemáticas en Egipto c. 1650 a.C.), y el Shulba Sutras (Matemáticas en la India c. 800 a.C.). Todos estos textos tratan sobre el Teorema de Pitágoras, que parece ser el más antiguo y extendido desarrollo matemático después de la aritmética básica y la geometría.

Éste es el plimpton322

Esta imagen es el Papiro de Moscú

Este es Pitágoras

Tradicionalmente se ha considerado que la matemática, como ciencia, surgió con el fin de hacer los cálculos en el comercio, para medir la Tierra y para predecir los acontecimientos astronómicos. Estas tres necesidades pueden ser relacionadas en cierta forma a la subdivisión amplia de la matemática en el estudio de la estructura, el espacio y el cambio.

Las matemáticas egipcias y babilónicas fueron ampliamente desarrolladas por la matemática helénica, donde se refinaron los métodos (especialmente la introducción del rigor matemático en las demostraciones) y se ampliaron los asuntos propios de esta ciencia.[1] Las matemáticas en el Islam, a su vez, desarrollaron y extendieron las matemáticas conocidas por estas civilizaciones ancestrales. Muchos textos griegos y árabes de matemáticas fueron traducidos al latín, lo que llevó a un posterior desarrollo de las matemáticas en la Edad Media.

Retrato helenístico-Séneca.

No se sabe con seguridad a quien retrata esta magistral cabeza. Hay quien apunta que podría tratarse de Eurípides, otros creen que representa a Calímaco, un matemático de Alejandría. Sea lo que fuere, esta cabeza, nos muestra la tendencia realista que se da en el arte rodio del siglo II. En ella, se representa la crudeza de la vejez con un intenso expresionismo.

 

Desde tiempos ancestrales hasta la Edad Media, las ráfagas de creatividad matemática fueron seguidas, con frecuencia, por siglos de estancamiento. Pero desde el Renacimiento italiano, en el siglo XVI, los nuevos desarrollos matemáticos, interactuando con descubrimientos científicos contemporáneos, fueron creciendo exponencialmente hasta el día de hoy.

b) Periodos de las matemáticas elementales: A continuación del anterior, se prolonga desde los siglos VI-V a.C. hasta finales del siglo XVI. Durante este periodo se obtuvieron grandes logros en el estudio de las matemáticas constantes, comenzando a desarrollarse la geometría analítica y el análisis infinitesimal.

   -IMPERIO MUSULMÁN: Durante el primer siglo del imperio musulmán no se produjo ningún desarrollo científico, ya que los árabes, no habían conseguido el impulso intelectual necesario, mientras que el interés por el saber en el resto del mundo, había desaparecido casi completamente. Fue a partir de la segunda mitad del siglo VIII, cuando comenzó el desenfrenado proceso de traducir al árabe todas las obras griegas conocidas. Se fundaron escuelas por todo el Imperio, entre las que destaca Bait Al-Hikma (Casa de la Sabiduría). Entre los miembros de esta escuela destaca un nombre propio Mohammed ibn-Musa Al-Khowarizmi que escribió más de media docena de obras matemáticas y astronómicas, dos de las cuales han tenido especial importancia en la historia. La primera de ellas está basada en una traducción árabe de Brahmagupta y en la que se da una reproducción exacta del sistema de numeración hindú, lo que ha originado la creencia popular de que nuestro sistema de numeración procede del árabe. El "nuevo" sistema de numeración vino a ser conocido como "el de Al-Khowarizmi" y a través de deformaciones lingüísticas derivó en "algorismi" y después en algoritmo, término que, actualmente, posee un significado mucho más amplio. Igualmente, a través del titulo de su obra más importante, el Hisab al-jabr wa-al-muqabala, nos ha transmitido otro nombre mucho más popular, la palabra "álgebra". En esta obra se estudian seis tipos de ecuaciones cuadráticas, así como un sin fin de elementos griegos.

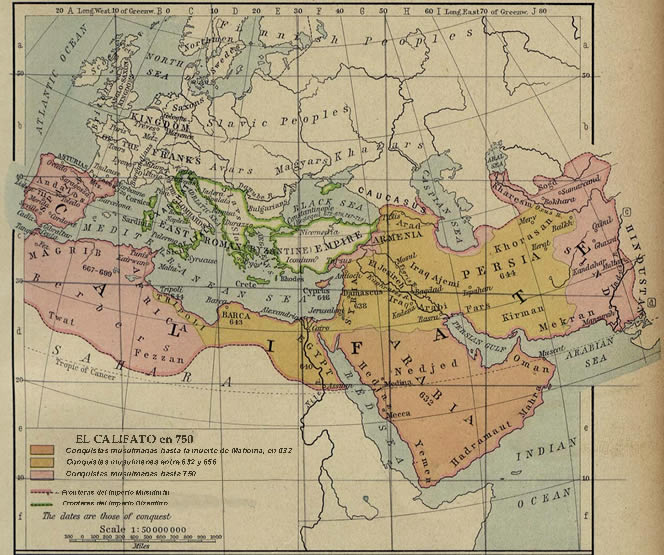Imperio musulmán Al-Khowarizmi, miembro

Escuela de Bait Al-Hikma

Con posterioridad a Al-Khuwarizmi se desarrollaron infinidad de procedimientos de cálculo y algoritmos especiales, entre ellos: - obtención del número pi con 17 cifras exactas mediante polígonos inscritos y circunscritos en la circinferencia realizada por Kashi (s. XV). Después de más de 150 años, en 1593, en Europa, Viète encontró sólo nueve cifras exactas. Hubo que esperar a fines del siglo XVI y comienzos del XVII para repetir el cálculo de Kashi. - cálculo de raíces por el método conocido actualmente como de Ruffini-Horner, posiblemente como resultado de la estrecha colaboración con los matemáticos chinos. Además fue advertida y expresada la serie del desarrollo binomial y fue también enunciada la tabla de coeficientes binomiales. - extracción aproximada de raíces, utilizando la interpolación lineal. - sumación de progresiones aritméticas y geométricas.

Viète

Asimismo, en virtud de la frecuente aplización en los cálculos de las irracionalidades, el límite entre los números racionales y los irracionales comenzó a difuminarse, ampliándose la concepción de número real positivo. La idea de una concepción única del número real obtuvo pues, en el oriente Medio cierto perfeccionamiento. Los trabajos algebraicos árabes entre los siglos IX-XV además de la resolución de ecuaciones de primer y segundo grado, incluían también las ecuaciones cúbicas. A estas últimas conducían diferentes tipos de problemas como la división de la esfera por un plano, la trisección del ángulo, la búsqueda del lado de un polígono regular de 9 lados... Otra dirección en la resolución de ecuaciones cúbicas, se basaba en la obtención de la imagen geométrica de la raíz positiva, por medio de la intersección de secciones cónicas, convenientemente elegidas. Sin embargo el gran defecto del álgebra de esta época era la ausencia de una simbología, lo que contuvo el desarrollo del álgebra. Además de la separación del álgebra, el rasgo característico más importante de las matemáticas árabes fue la formación de la trigonometría. En relación con los problemas de astronomía, confeccionaron tablas de las funciones trigonométricas con gran frecuencia y alto grado de exactitud, tanto en trigonometría plana como esférica. Entre las obras geométricas destacan las de Omar Khayyam (s. XVI) y Nasir Edin (s. XIII), directamente influenciadas por las obras clásicas, pero a las que contribuyeron con distintas generalizaciones y estudios críticos, como los relativos al axioma euclideano del paralelismo, que pueden considerarse como estudios precursores de la geometría no euclideana.

Omar-Khayyam

  -EUROPA MEDIEVAL Y EL RENACIMIENTO. En el continente europeo, las matemáticas no tienen un origen tan antiguo como en muchos países del Lejano y Medio Oriente, alcanzando sólo éxitos notorios en la época del medievo desarrollado y especialmente en el Renacimiento. El punto de arranque de las matemáticas en Europa fue la creación de los centros de enseñanza. Con anterioridad, tan solo algunos monjes se dedicaron a estudiar las obras de ciencias naturales y matemáticas de los antiguos. Uno de los primeros centros de enseñanza fue organizado en Reims (Francia) por Gerberto (Silvestre II) (940-1003). Fue posiblemente el primero en Europa que enseñó el uso de los numerales hindú-arábigos. Sin embargo hubo que esperar a que los musulmanes rompieran la barrera lingüística, hacia el siglo XII, para que surgiera una oleada de traducciones que pusieran en marcha la maquinaria matemática. El trabajo de los traductores fue sensacional. Así Gerardo de Cremona (1114-1187) tradujo del árabe más de 80 obras. Durante el siglo XIII surgió la figura de Leonardo de Pisa (1180-1250) más conocido como Fibonacci. Alrededor del año 1202 escribió su célebre obra "Liber Abaci" (el libro del ábaco), en el que se encuentran expuestos: el cálculo de números según el sistema de numeración posicional; operaciones con fracciones comunes, aplicaciones y cálculos comerciales como la regla de tres simple y compuesta, la división proporcional, problemas sobre la determinación de calidad de las monedas; problemas de progresiones y ecuaciones; raíces cuadradas y cúbicas... Fibonacci quedó inmortalizado por la famosa "sucesión de Fibonacci" y el famoso problema de los conejos. Otra obra importante fue el "Practica Geometriae" dedicada a resolver problemas geométricos, especialmente medida de áreas de polígonos y volúmenes de cuerpos. Otro contemporáneo, aunque no tan excepcionalmente dotado fue Jordano Nemorarius (1237-?) a quien debemos la primera formulación correcta del problema del plano inclinado. El profesor parisino Nicole Oresmes (1328-1382) generalizó el concepto de potencia, introduciendo los exponentes fraccionarios, las reglas de realización de las operaciones con ellos y una simbología especial, anticipándose de hecho a la idea de logaritmo. En una de sus obras llegó a utilizar coordenadas rectangulares, aunque de forma rudimentaria, para la representación gráfica de ciertos fenómenos físicos.

Fibonacci              Geberto

Ya en el siglo XV, época de las grandes navegaciones, la trigonometría fue separada de la astronomía, alzándose como ciencia independiente de la mano de Regiomontano (1436-1474), que trató de una manera sistemática todos los problemas sobre la determinación de triángulos planos y esféricos.
Regiomontano enriqueció además el concepto de número, introduciendo los radicales y las operaciones con ellos, ampliando así las posibilidades de resolución de ecuaciones. Nicolo Tartaglia (1500-1557), Fiore y Scipión del Ferro (1456-1474) desarrollaron fórmulas para la búsqueda de ecuaciones de tercer grado.
Pero fue Jerónimo Cardano (1501-1576) quien introdujo un método regular de resolución de ecuaciones de tercer y cuarto grado en su obra "Ars Magna". En esta obra se expresan diversos teoremas que relacionan raíces y coeficientes, así como la divisibilidad de un polinomio por factores (x-x₁), donde x₁ es raíz del polinomio. Asimismo en esta obra se establece un notable cambio desde el álgebra literal al álgebra simbólica.

Nicole Tartaglia  Jerónimo Cardano

Fue François Viète (1540-1603) quien dio un sistema único de símbolos algebraicos consecuentemente organizado, gracias al cual resultó por primera vez posible, la expresión de ecuaciones y sus propiedades mediante fórmulas generales. Viète estableció en todo momento, una fuerte conexión entre los trabajos trigonométricos y algebraicos, de forma que de igual manera que se le considera el creador del álgebra lineal, se le podría considerar como uno de los padres del enfoque analítico de la trigonometría, esto es, la goniometría. Para hacer más fáciles los cálculos, los matemáticos desarrollaron ciertos procedimientos en los que, el papel fundamental lo jugaban determinadas relaciones trigonométricas, lo que llevó a la confección de numerosas tablas trigonométricas. En la elaboración de tablas trabajaron, por ejemplo, Copérnico (1473-1543) y Kepler (1571-1630). Semejantes métodos se utilizaban tan frecuentemente que recibieron el nombre de "prostaferéticos". Ellos fueron utilizados por los matemáticos de Oriente Medio, Viète, Tycho Brahe, Wittich, Bürgi y muchos otros.
Estos métodos siguieron utilizándose incluso después de la invención de los logaritmos a comienzos del siglo XVII, aunque sus fundamentos, basados en la comparación entre progresiones aritméticas y geométricas, comenzaron a fraguarse mucho antes. En 1614 fue publicada por John Neper (1550-1617) la obra "Canonis mirifici logarithmorum descriptio" y en ella las primeras tablas de logaritmos de funciones trigonométricas.
Años más tarde, en estrecha colaboración con Henry Briggs (1561-1630) desarrollaron el sistema logarítmico decimal. La teoría de las funciones logarítmicas fue seguidamente desarrollada, alcanzando su culminación en los trabajos de Leonard Euler. Junto a estos avances científico-matemáticos comenzaron a desarrollarse las primeras máquinas de cálculo.

c) Periodo de formación de las matemáticas de magnitudes variables: El comienzo de es periodo está representado por la introducción de las magnitudes variables en la geometría analítica de Descartes y la creación del cálculo diferencial e integral en los trabajos de I. Newton y G.V. Leibniz. En el transcurso de este periodo se formaron casi todas las disciplinas conocidas actualmente, así como los fundamentos clásicos de las matemáticas contemporáneas. Este periodo se extendería aproximadamente hasta mediados del siglo XIX.

d) Periodos de las matemáticas contemporáneas: En proceso de creación desde mediados del siglo XIX. En este periodo el volumen de las formas espaciales y relaciones cuantitativas abarcadas por los métodos de las matemáticas han aumentado espectacularmente, e incluso podríamos decir exponencialmente desde la llegada del ordenador.

Las distintas ramas que analizaremos son:
a) Álgebra y aritmética:  En la antigüedad, el Álgebra fue una parte inseparable de la Aritmética, más tarde se separó de ella. Ésta es la razón por la que en gran parte de la literatura científica a la hora de estudiar ambas ramas se hace de una manera conjunta. La aritmética será la ciencia que se ocupa de los objetos concretos, esto es, de los números. En cambio el Álgebra es, en esencia, la doctrina de las operaciones matemáticas analizadas desde un punto de vista abstracto y genérico, independientemente de los números o objetos concretos.
b) Análisis matemático
c) Geometría La historia del origen de la Geometría es muy similar a la de la Aritmética, siendo sus conceptos más antiguos consecuencia de las actividades prácticas. Los primeros hombres llegaron a formas geométricas a partir de la observación de la naturaleza.
El sabio griego Eudemo de Rodas, atribuyó a los egipcios el descubrimiento de la geometría, ya que, según él, necesitaban medir constantemente sus tierras debido a que las inundaciones del Nilo borraban continuamente sus fronteras. Recordemos que, precisamente, la palabra geometría significa medida de tierras.